Viscous Dissipation and Criticality of Subducting Slabs
Michael R. Riedel, Shun Karato, Dave A. Yuen
We calculate the amount of viscous dissipation
during subduction of a lithospheric plate
as constrained by experimental rock mechanics.
The maximum bending moment Mcrit that can be sustained by a slab
is of the order of 1019 Nm per m
according to Mcrit ~ sp * h2/4,
where sp is the Peierl's stress limit of slab materials and
h is the slab thickness.
Near Mcrit, the amount of viscous dissipation
grows strongly as a consequence of a lattice
instability of mantle minerals (dislocation glide in olivine).
The value of Mcrit is about 1-2 orders of magnitude too high to
be reached by a ridge push of typically 1012 N per m
at convergent plate boundaries, but unusual tectonic
settings like a thick sedimentary load of the lithosphere
or a shallow angle of slab penetration at the transition zone
can help to overstep this bending moment threshold.
The immediate consequence is a sudden drop of the effective
viscosity to below 1021 Pas, so that the observed
weakening effect serves as a self-regulating mechanism to adjust
plate tectonics on Earth against strong viscous resistance forces.
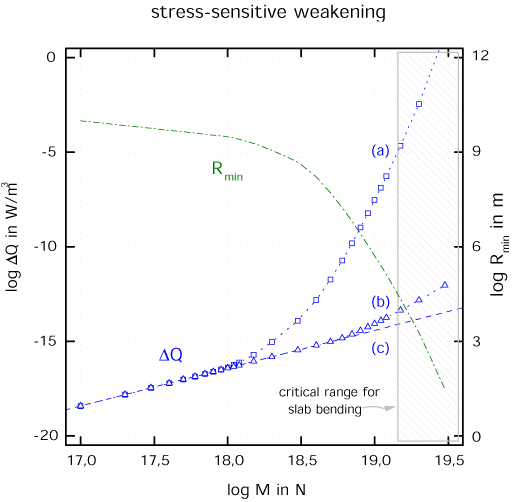
Strong growth of viscous dissipation DeltaQ
in dependence of the bending moment M for 3 different sets
of constitutive equations for olivine creep (subduction speed
10 cm/yr, slab thickness 85 km):
(a) complete set including Peierls mechanism
(b) reduced set: only diffusion and power-law creep included
(c) linear rheology: only diffusion creep included
Also shown is the minimum slab bending curvature Rmin in dependence
of M.
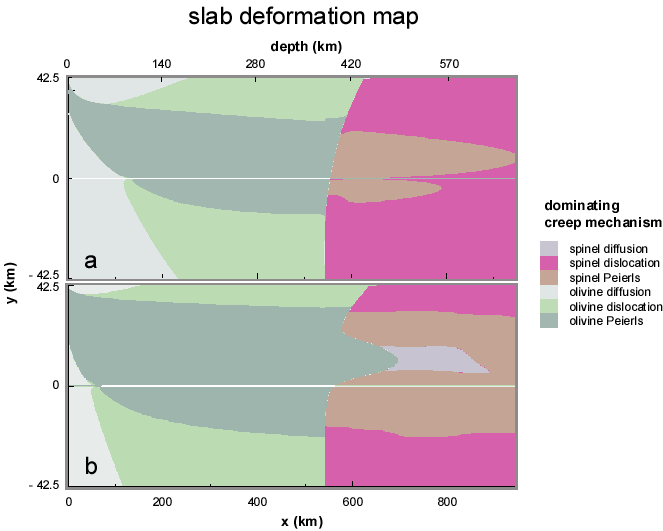
Dominant deformation mechanisms in subducting slabs.
Initial temperature distribution corresponds to that for a 100
myr oceanic lithosphere of 85 km thickness. The cases for
subduction velocities of 4 cm/yr and 10 cm/yr are shown. Because
stress, temperature, pressure and grain-size change
significantly in space for a given slab, dominant mechanisms of
deformation change in a complicated fashion. In high stress,
low temperature regions, the Peierls mechanism dominates. In
moderate stress, moderate to large grain-size-regions, power-
law creep dominates. Diffusion creep plays an important role in
cold, fine-grain regions in the center of labs after a phase
tranformation. Note that such a pattern also depends on the
velocity of subduction, which controls the temperature
distribution and the magnitude of stress.
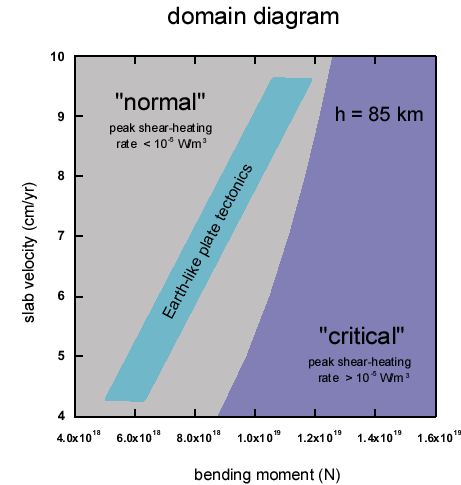
Domain diagram showing the critical range of bending moments
for a slab with 85 km thickness where the
lithosphere is subject to thermo-mechanical
instabilities (peak shear-heating rate inside the slab larger
than 10-5 W/m3).
In this ``critical'' domain,
the minimum local bending curvature
of the slab Rmin drops down to values below the slab thickness h.
Arrows indicate the possible effect of the presence of water in the mantle lithosphere
(see discussion).
Also shown is the range of plate-like
tectonics on Earth as inferred from observation



